研究の特徴

主要研究テーマ

エネルギーシステムの安全性，経済性に関する熱流動現象の理解とその応用

エネルギーシステムの安全性の向上とは？

配管を流れる流体が管壁の鉄イオンを流れ場に拡散させ、配管が減肉してそこから破断が起こります。高温高圧の蒸気が流れている場合には、人命にかかわる大きな事故につながります。
＝＞どうして鉄イオンの拡散が促進されるのかを明らかにします。どのような流れを作らないようにすることが安全性を高めるのかを研究します。
原子炉での事故が起こった場合に、格納容器を「受動的」（人の手を介することなく）に安全に冷却する方法を考えています。
＝＞電気などの外部動力を使うことなく、自然界の法則（重力、浮力、表面張力など）のみに従う方法を考えています。
計算では決して被害を受けないように設計された巨大風車が、倒壊する事故が多数起こっています。なぜこのような被害は起こるのでしょうか？
＝＞突風など乱れた流れ（乱流）の性質が分かっていません。乱流の性質を詳しく調べます。

私たちの身の回りには、エネルギーを生み出す機器やエネルギーを利用する機器がたくさんあります。それらに関連した施設を含めて「システム」と呼ぶことにします。自動車のエンジン、航空機のタービン、水力発電、燃料電池、などなど。一見して関係ないところにも、熱流体の知識は利用されています。安全性をさらに向上させるために、より熱流体の知識を活用し、より深く研究をすすめていきます。

エネルギーシステムの経済性の向上とは？

巨大なタンカーが石油を満載して、中東と日本の間を往復しています。船体の表面（固体）と海水（液体）の間には、摩擦（抵抗）が働きます。この摩擦をわずか数％減らすだけで、絶大な経費の節約につながります。異なる層が接する界面には必ず摩擦抵抗が働きます。
＝＞摩擦を減らすためには、どのような工夫があるのかを流体の知識を使って考えています。これによって、省エネを実現する方法を提案します。
リニアモーターカーや核融合装置に利用される超伝導マグネットは、極低温まで冷却する必要があります。液体ヘリウムの流し方によって高効率な冷却ができます。
＝＞液体ヘリウムの流れは、超流動乱流と呼ばれ、量子渦の振る舞いなど未知なるベールに包まれています。超流動乱流の基礎的性質を実験的に調べます。
熱を効率的に伝えたり、放熱する機器にヒートパイプやヒートスプレッダがあります。
＝＞沸騰、凝縮をする表面の組成を変えること、特に液体と固体が接する濡れ性を変化させることが有効な方法と考えられています。

流体の流れや熱の移動を少し変える工夫をすると、エネルギーを有効に利用することができます。

カラースクリーン法
曳航水槽実験
容器内熱対流
自由界面波

なぜ、乱流を研究するのか？

古典力学最後の難問：乱流現象の理解に向けて

　イギリスのホーレスラム卿は、完全流体に関するポテンシャル理論を中心とする多くの論文成果を取り纏め、1932年にHydrodynamics(第６版)を出版した。しかし、書籍の中ではその後の流体力学の中心となる乱流についてはほとんど述べられてはいない。ラム卿は乱流について無関心であったわけではなく、第６版の完成後、彼は“私は老人であり間もなく天国に招されるであろう。その時天界の隅から気に掛かる２つの点がある。１つは電気量子力学であり、もう一つは乱流である。私は前者については楽観的であるが、後者については悲観的である”と語ったといわれる（「流体力学」日野幹雄著より）。その後の彼の予言は的中したのである。

　量子力学と流体力学は関係ないように思われるが、量子力学の発展に貢献したHeisenbergは、層流・乱流の安定性に関する学位論文を書いており、エネルギースペクトル型を提示している。また、相対性理論を構築したEinsteinはブラウン運動に関するコロイド粘性理論を1905年5月に奇跡の年の第二論文「静止した流体に浮かぶ微粒子に熱の分子運動論が要求する運動」として投稿している。その中で彼は流体の浸透圧の考え方を使っている。また、近年の動向として、「量子流体力学」という新たな研究対象も注目される。

Lam 流体力学　第６版

数学のミレニアム問題の１つ：流体の運動方程式Navier-Stokes方程式

　2000 年 5 月にアメリカのクレイ研究所は、21 世紀の始まりとともに次の千年（ミレニアム）に取り組むべき数学の 7 つの未解決問題への挑戦を宣言した。クレイ研究所が提唱した７つの問題には、それぞれの解決に百万ドルの懸賞金がかけられている。いずれも数学において取り組むべき重要な課題であり、7 つの問題のうち「ポアンカレ予想」はすでに肯定的に解決され、残る 6 問が未解決である。その未解決問題の一つが、流体の運動方程式である「ナヴィエーストークス方程式の解の存在問題」である。

　ナヴィエーストークス方程式は三次元の偏微分方程式であり、「3次元の場合に滑らかな初期値から出発して、いつか有限時間内に何らかの特異点が発生するかどうか」、という問題である。

天気予報はなぜ当たらないのか？　台風の進路予測はなぜ難しいのか？

　明日の天気は気象庁にあるスーパーコンピュータで計算されている（数値予測）。空気の流れ、海洋の流れ、水蒸気や熱の移動などを対象にしている。その中核をなすのが流体の運動であり、Navier-Stokes方程式である。Navier-Stokes方程式は、ミレニアム問題に掲げられているように三次元空間において解析的な解を任意の初期に対して得られない。そこで、方程式を離散化することで、数値解を見出している。対象とするスケールは、地球規模の1万メートルから最小の渦スケールは0.1mmまでの11桁である。全地球の表面を最小渦が解像できるほど細かな格子に離散化をすることは、最新のスーパーコンピュータ「富岳」でも不可能である。そのため、大きなスケールのみを再現できる数値モデルを用いることになり、モデルによって結果もおのずと異なってくる。１週間先の天気予報が当たらないことは驚きではないが、明日の天気がそこそそ当たるのは私には驚きである。

乱流の属性と普遍性

　そもそも、乱流には定義が存在しない。乱流の属性を掲げることで、乱流とはどういう現象かを理解している。例えば、

強い非線形性
初期値鋭敏性、予測不可能性
間欠的な強いエネルギー散逸を伴う
時空間(４次元)に及ぶ現象

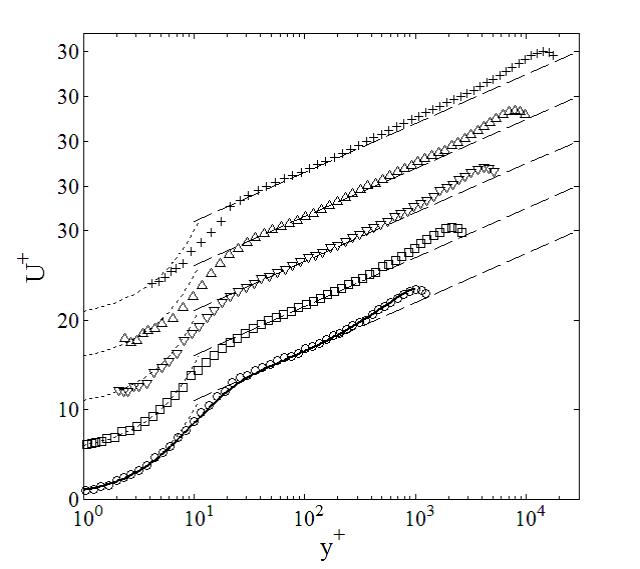
　乱流は一見して複雑に乱れた無秩序の流れという印象であるが、ときおり普遍的な美しい一面と垣間見せてくえる。例えば、壁に接する流れは、平均速度分布が滑らかに変化する境界層が存在する。壁からの距離y+と平均速度U+（記号+は壁変数での無次元化）をプロットすると、きれいな対数関係が現れる。滑らかな壁に接する流れでは、試験管の中の流れから、飛行機の翼の上の流れまで同じである（流れの種類によらない）。もっと大きな地球規模の流れでも成り立つと考えられている。しかし、どうしてこのような美しい関係が、一見して乱雑な乱流に潜んでいるのだろうか？

壁乱流の対数速度分布（記号の違いはレイノルズ数の違い）

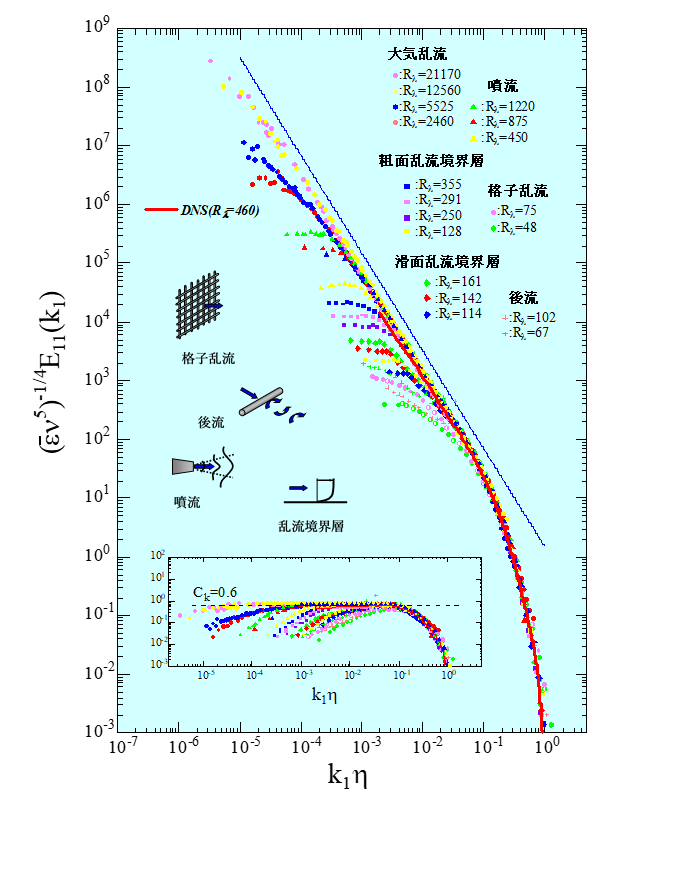
　もう一つ乱流の普遍性を紹介しておこう。下図はエネルギースペクトルを波数に対してプロットしたグラフである（縦軸・横軸とも無次元化してある）。大きな渦（小さな波数）から小さな渦（大きな波数）までエネルギーが流れていく（カスケード）様子を統計的にあらわしている。境界層、噴流、後流、など乱流の種類によらずに傾きは-5/3乗に比例して同じ直線に載っている。この美しい関係は、乱流のどのような性質から決まってくるのだろうか？

乱流のエネルギースペクトル 3

　壁に沿う流れの対数速度分布やエネルギースペクトルの-5/3乗則など、乱流の普遍性が現れる要因を知りたい！その物理的な要因がわかれば、乱流現象をより正確に予測して操る(制御する)ことが可能になる。幅広い応用研究につながるであろう。

数値計算によって乱流（Navier-Stokes方程式の解）を見る

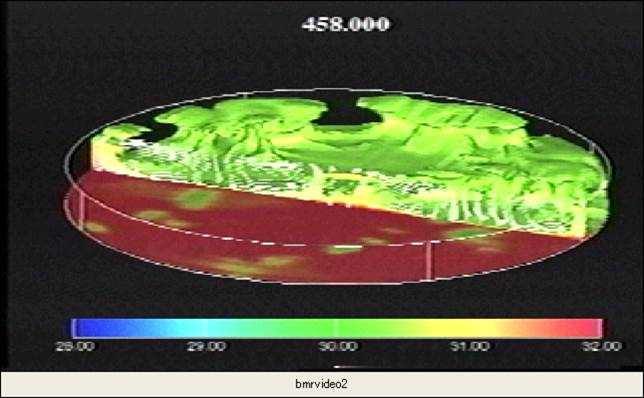
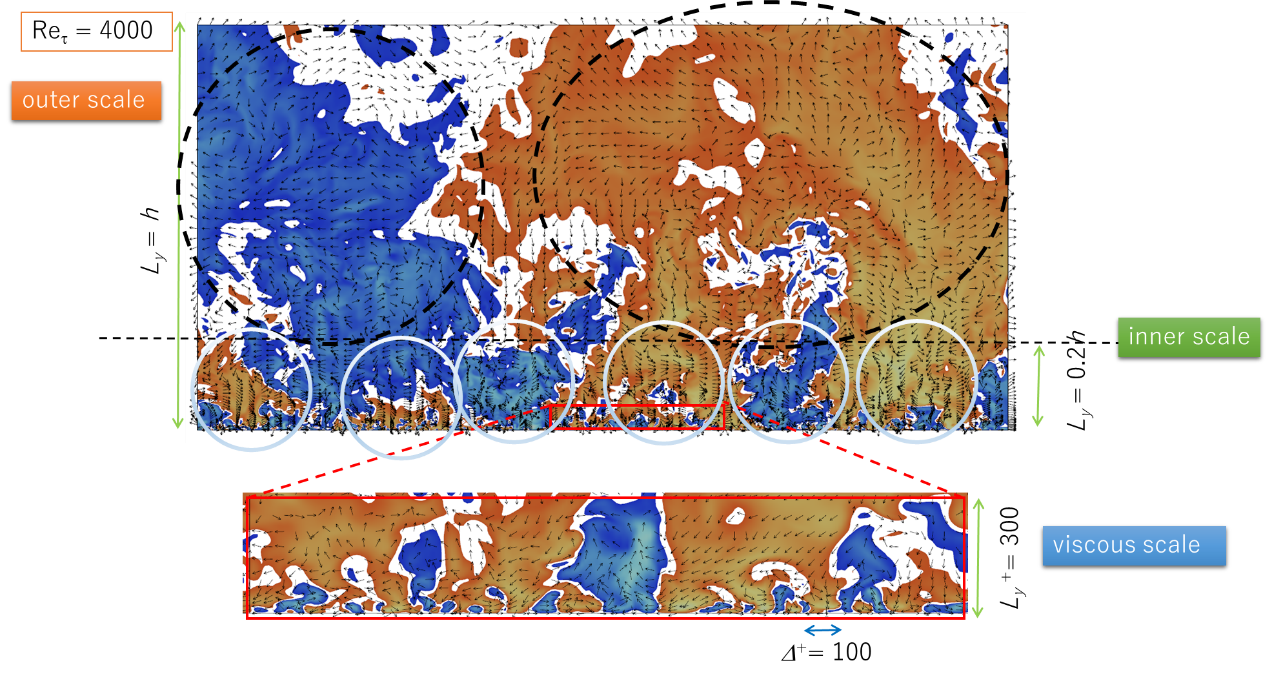
　寺田寅彦は「物理学序説」の中に「流体力学の専門家はその古色蒼然たる基礎方程式を通してのみしか流体を見ないから,何時迄たってもその方程式に含まれていない種類の現象に目の明く日は来ない。」と書いている。寺田の時代から、状況が少し変わったとすれば、私たちは基礎方程式を通して視覚的に現象を理解できることがなったことでろうか。 Navier-Stokes方程式の解は、解析的に求まらない。しかし、スーパーコンピュータによる数値計算から、限られた条件下での乱流現象を視覚的に理解できるようになっている。下図は、壁に沿う流れの速度に色付けをしたものである。壁から離れた大きな構造が壁近くの小さな構造へ階層的に分布していることが理解できる。「百聞は一見に如かず」と言ところであろうか。対数速度分布の背景には、乱流構造の相似的な分布がありそうである。この構造を制御すれば、。。。というふうに夢は膨らむ。

壁乱流の組織構造（色の違いは低速と高速流体領域、山梨大学　山本義暢氏）3

乱流現象を理解するためのデータ解析入門として、以下の文献をご覧ください。

（１）講座：流体乱流研究から診たプラズマ乱流データの解析
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_09/jspf2009_09-618.pdf
第２章相関とスペクトル解析
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_09/jspf2009_09-620.pdf
第３章確率密度関数とその応用
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_10/jspf2009_10-665.pdf
第４章組織構造の定義とその抽出
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_11/jspf2009_11-774.pdf
第５章流体およびプラズマ乱流の普遍性
http://www.jspf.or.jp/Journal/PDF_JSPF/jspf2009_11/jspf2009_11-783.pdf

（２）〔特集〕乱流を測る－乱流理解に貢献する計測技術の最前線・課題・展望－
乱流の普遍則とその解明を支える実験技術, ながれ37（2018）245－254
https://www.nagare.or.jp/download/noauth.html?d=37-3_tokushu4.pdf&dir=133